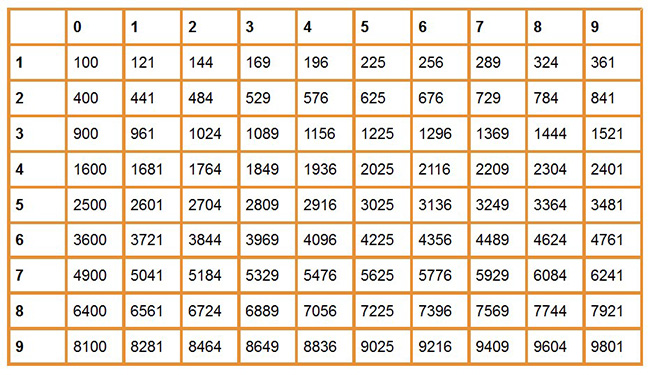
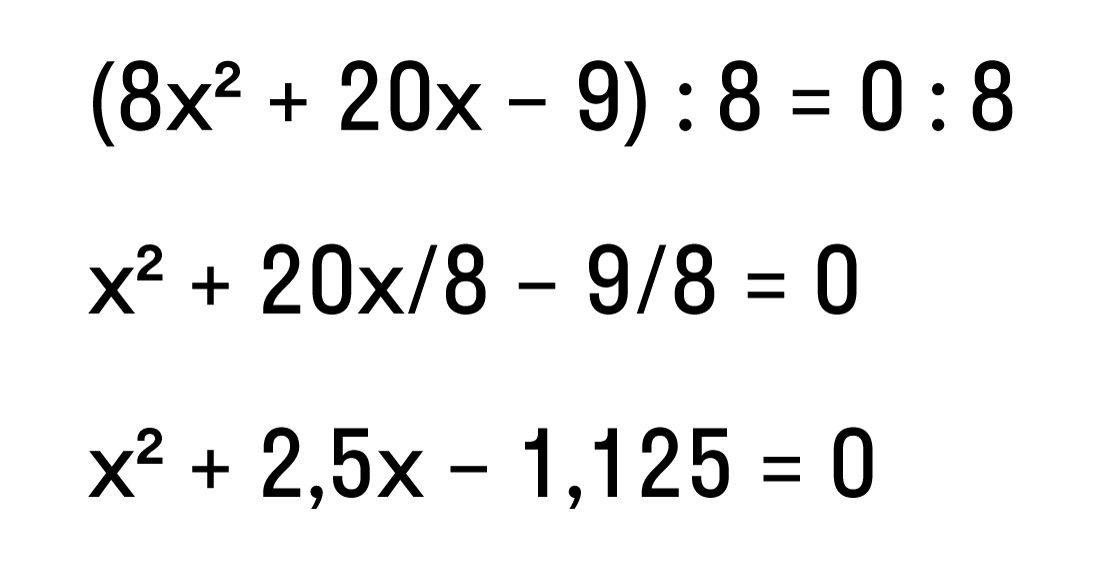Дано натуральное число является ли оно точный квадрат

Простые и составные числа
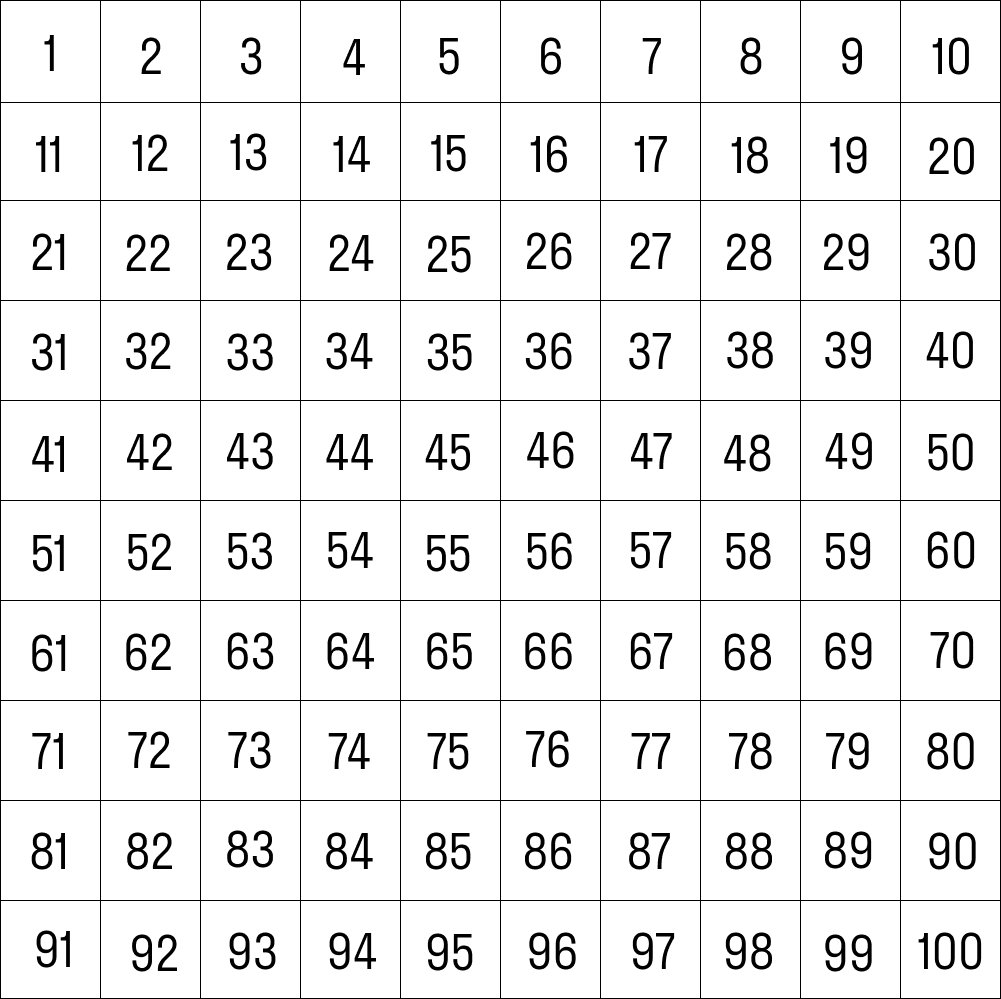
Натуральные числа, имеющие ровно два различных делителя единицу и само это число , называются простыми. Натуральные числа, которые можно разложить в произведение двух множителей, больших единицы, называются составными. Обвести двойку и вычеркнуть все остальные числа, делящиеся на 2 4, 6, 8, …. Затем обвести первое невычеркнутое число и вычеркнуть все остальные числа, делящиеся на него. И продолжать эту процедуру, пока не будет достигнут конец списка. Теперь все невычеркнутые числа в списке — простые.









Даны два целых числа. Выведите значение наибольшего из них. Ввод Вывод 3 7 7 2 2 2 B: Какое число больше? Программа должна вывести число 1, если первое число больше второго, число 2, если второе больше первого или число 0, если они равны. Ввод Вывод 4 5 2 Эту задачу желательно решить с использованием инструкций if

=n²..gif/220px-The_sum_of_the_first_n_odd_integers_is_n²._1+3+5+...+(2n-1)=n²..gif)
.png)
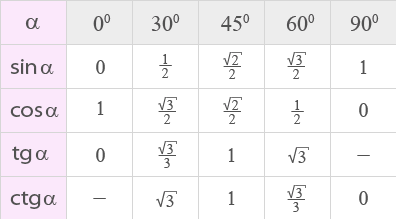


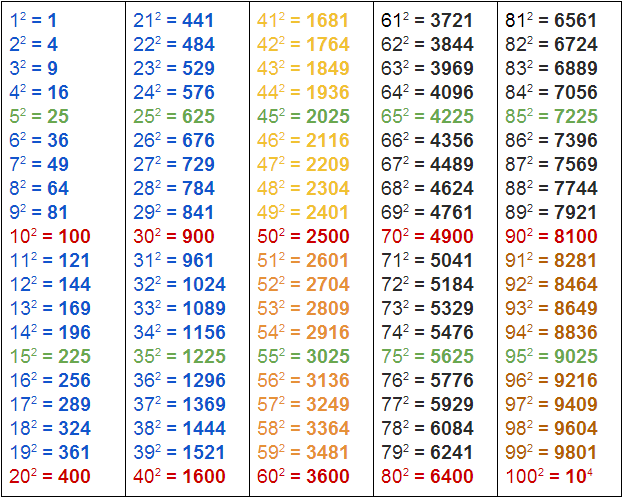
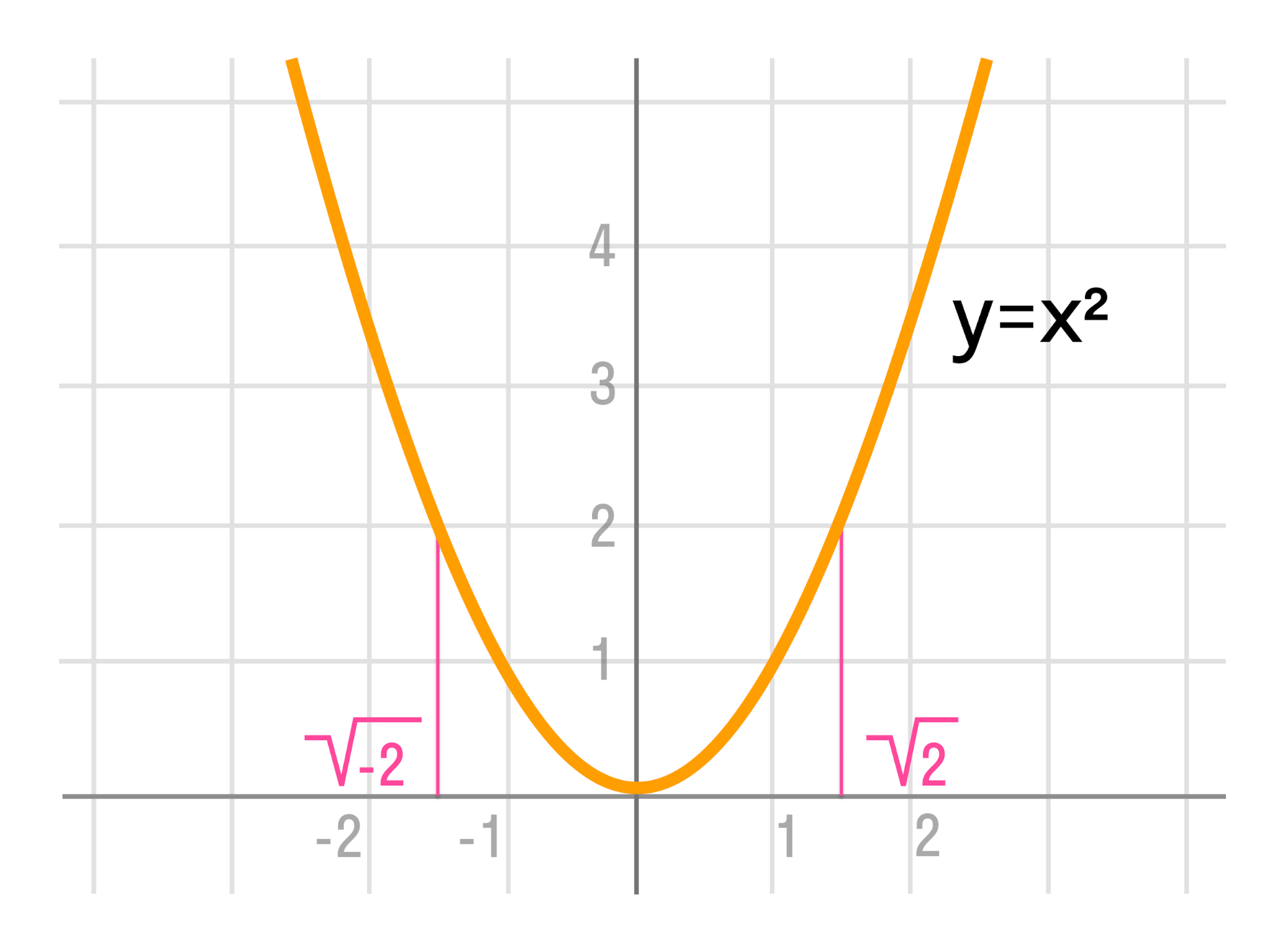
| 148 | Полный квадрат , также точный квадрат или квадратное число , — число, являющееся квадратом некоторого целого числа. | |
| 80 | Точнее, от вашего браузера их поступает слишком много, и сервер VK забил тревогу. Обратитесь в поддержку сервиса. | |
| 121 | Код python. Код go. | |
| 184 | Попробуйте повторить позже. Натуральные числа от 1 до 8 расставили по кругу так, что каждое число делится на разность своих соседей. |
Попробуйте повторить позже. Назовем натуральное число хорошим, если оно делится на два последовательных нечетных натуральных числа, больших Докажите, что для любого натурального среди чисел от до менее чисел являются хорошими. Заметим, что число, делящееся на два последовательных нечётных натуральных числа, делится также на их произведение. Поэтому количество чисел от до делящихся на фиксированных нечётных числа и не превосходит Также заметим, что число, не превосходящее может делиться на только в случае, когда Обозначим наибольшее нечетное число, не превосходящее через то есть для него верно, что а также Тогда суммарное количество хороших чисел не превосходит.